AI 能制造爆款,却写不出好文章
AI写作的困境与Transformer技术解析 文章通过对比测试发现AI生成的文章在比喻、象征和非线性叙事方面明显逊色于文学大师作品。作者从技术角度分析指出,当前主流的大语言模型(LLM)基于Transformer架构,其采样策略(如Top-k和温度参数)影响了文本质量。温度参数T通过指数函数调节词汇概率分布,T值越小输出越保守,T值越大则越多样。虽然这些技术手段能控制文本生成,但仍难以达到人类作
缘起
最近公众号的质量就越来越差,每天的午饭都不香了,大约是 AI 惹的祸;遂把推流的公众号往 AI 检测工具一放,果不其然 100%,就说怎么不下饭,原来是没人味了。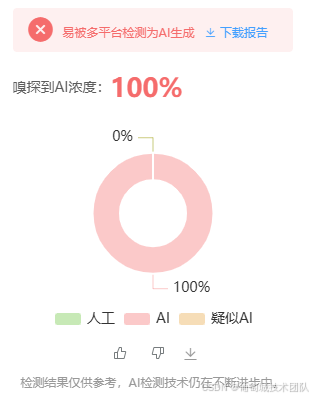
尝试
AI 就不能生成一些脍炙人口的文章吗? 上手!
1.先来写个比喻:
对比一下史铁生的:
日子总在过去,成为一张张作废的卡片。失恋,是一团烟雨,心灵的一道陌生又熟悉的布景
"心如刀绞"直接使用成语表达感受,没有新鲜感,平庸中缺乏深度。
2.象征:
对比一下鲁迅的:
秋天的后半夜,月亮下去了,太阳还没有出,只剩下一片乌蓝的天;除了夜游的东西,什么都睡着。华老栓忽然坐起身,擦擦火柴,点上遍身油腻的灯盏,茶馆的两间屋子里,便弥满了青白的光。
"要变天了"很直白,直接点题,不如 “擦火柴”、点灯这些暗示更有意境。
3.非线性叙事
对比一下马尔克斯的:
多年以后,奥雷连诺上校站在行刑队面前,准会想起父亲带他去参观冰块的那个遥远的下午
冲突直接被揭晓,撒了谎,开局整的和结尾一样,没有悬念感。
Transformer 初探
试了试,确实差点意思。我们从技术的角度看看,为啥会变成这样。
众所周知,现如今的 LLM 绝大多数都是基于 Transformer 架构的。
工作流程
我们先来粗略了解一下它的工作流程。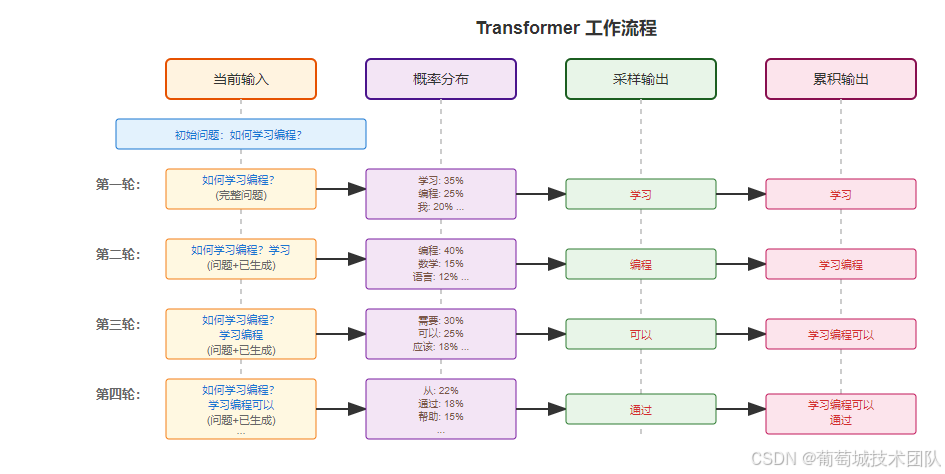
大约就是每次生成从候选词列表中选择一个 token 作为输出,这个这次输出作为下次输入。关键点在于采样输出是怎么选择的。
早期的 llm 通过 Top-k 加温度作为采样策略,后来引入了 Top-p 等其他负责的控制策略。
Top-k 采样
Top-k 比较简单,就是把候选词按照概率从高到低排,取前 k 个。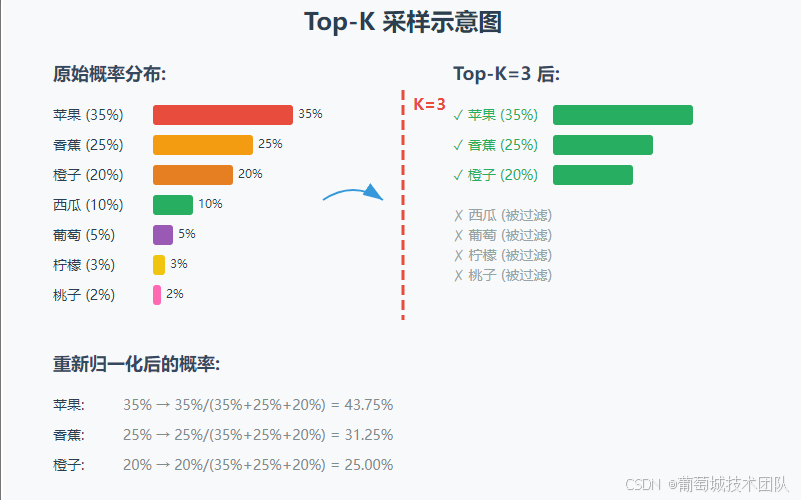
温度
假设只有 Top-k 采样,会发生什么?会变成每次都从k个元素中选择,而top1会被更高概率选择,导致输出重复度比较高。
为了让输出更加丰富,不这么单调,需要引入新的采样策略,让低概率的词也可能被选择到。
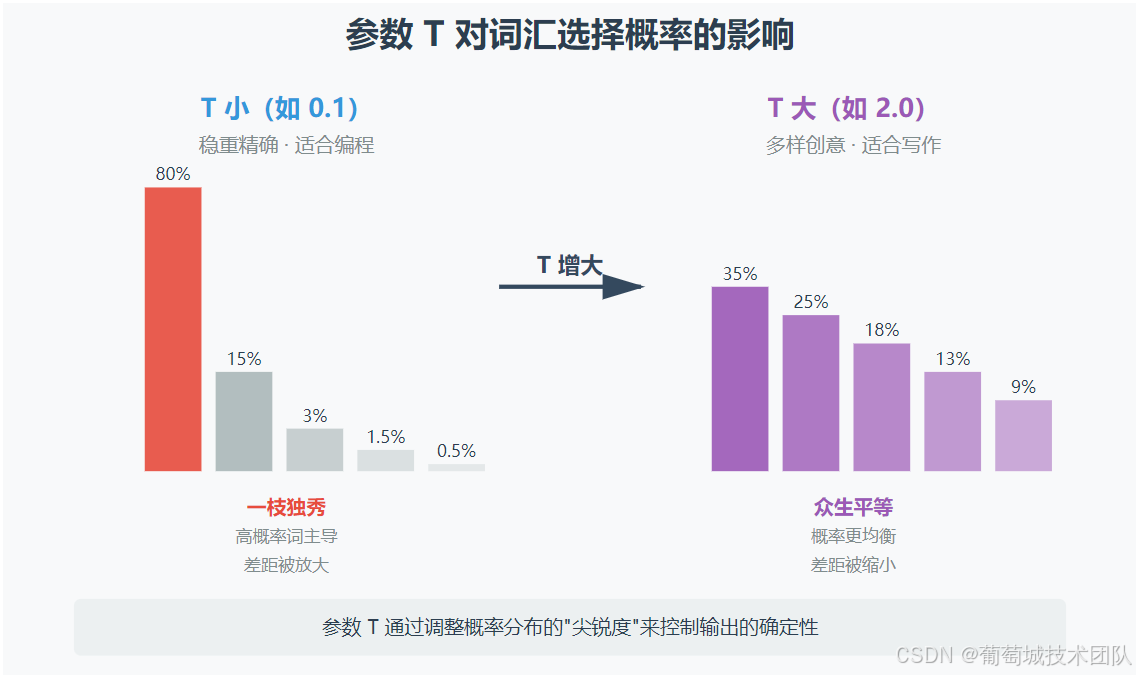
假设有一个参数,
-
值小的时候稳重一些,选择概率高的,应对一些严谨性高的场景(如编程)
-
值大的时候多样一些,选择概率低的,应对一些丰富性高的场景(如写作)
为了方便描述,我们姑且先称这个参数为T。
也就是说
-
T小的时候,我们需要让低概率词的被选择的机会变小,也就是放大低概率词和高概率词的差距,一枝独秀。
-
T大的时候,我们需要让低概率词的被选择的机会变大,也就是缩小低概率词和高概率词的差距,众生平等。
除法
什么运算可以实现这种缩放效果呢?最朴素的,就是除法。我们用 xix_ixi 表示词汇表中第 i 个词的概率(术语叫logits), yiy_iyi 表示第 i 个词温度调节后的概率,有下面这样的公式。
yi=xiT y_i = \frac{x_i}{T} yi=Txi
指数函数
我们知道,概率之和应该为1。为了让概率之和变为1,我们需要用 当前概率 除以所有概率的和得到新的概率(归一化)。
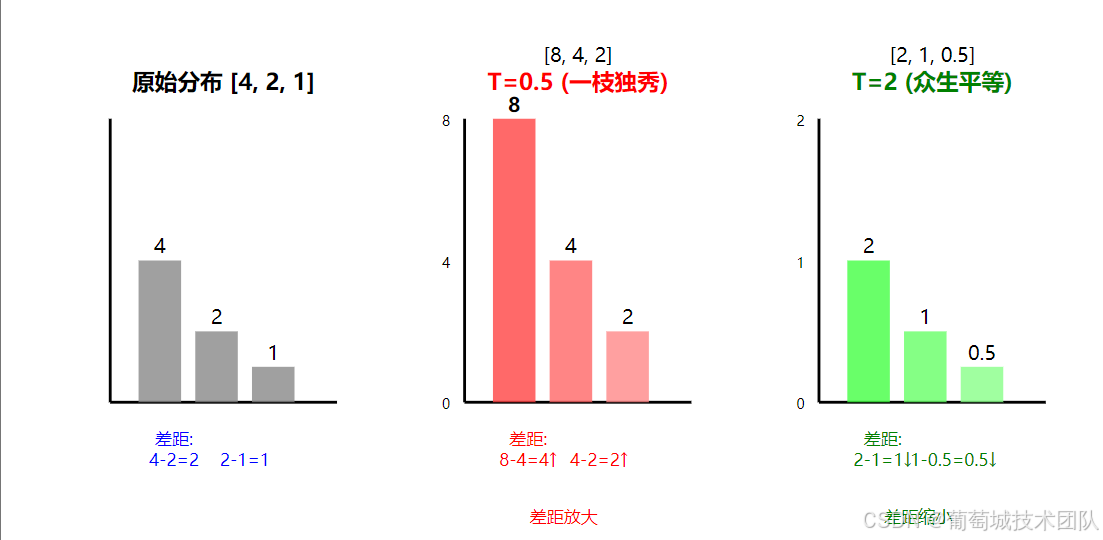
聪明的你可能已经想到了,等比例缩放一旦归一化,我们所有缩放都没有意义了。比如:[5,3,2] 无论我们怎么使用除法,归一化都会变成[0.5,0.3,0.2]。
显然,我们需要再引入一个非线性变化,让我们缩放不失效,我们选择使用指数函数。
zi=eyi z_i = e^{y_i} zi=eyi
举例说明一下
我们的缩放不再被归一化抵消,平均概率差距也被拉大了。
总结
这里我们已经得到了温度缩放的Softmax公式:
σ(x⃗)i=exiT∑j=1nexjT \sigma(\vec{x})_i = \frac{e^{\frac{x_i}{T}}}{\sum_{j=1}^{n} e^{\frac{x_j}{T}}} σ(x)i=∑j=1neTxjeTxi
这个公式对应上面提到的三个步骤:
- 使用除法实现缩放,即一枝独秀和众生平等。
yi=xiT y_i = \frac{x_i}{T} yi=Txi
-
zi=eyiz_i = e^{y_i}zi=eyi, 指数函数让缩放不被归一化抵消。
-
Pi=zi∑j=1nzjP_i = \frac{z_i}{\sum_{j=1}^{n} z_j}Pi=∑j=1nzjzi ,归一化过程(让所有概率的和为一)。
T为什么称之为温度呢?这里T小 对应稳重,T大对应活跃,这和温度的物理意义是一致的,温度越高,分子热运动越剧烈,随机性越强(熵越高)。
引入温度之后相同的问题,也会有不同的回答。
注意力机制
我们知道,一句话中不同词 贡献的信息量是不同的,相同的词在不同的句子中贡献的信息量也是不同的。举例说明:
- 她穿着蓝色外套。这里“蓝色”的信息量 要低于“外套”的信息量,它只是外套的形容词
- 桌上放着三把钥匙——蓝色的那一把能打开保险箱。这里“蓝色”的信息量就很高了,直接决定哪个钥匙是有用的。
这个信息量很好理解,但很难直观的使用数学描述,让我们换一个形式表述问题,对于要预测的下一个词, 我们需要知道哪些词 和我们要预测的词相关度更高。
这些词在底层是使用向量存储的,我们怎么判断两个向量是否相关呢?没错,就是看向量的夹角,夹角为90度就毫无关系,为0度就是高度相关。
进而,我们使用投影来计算相关度。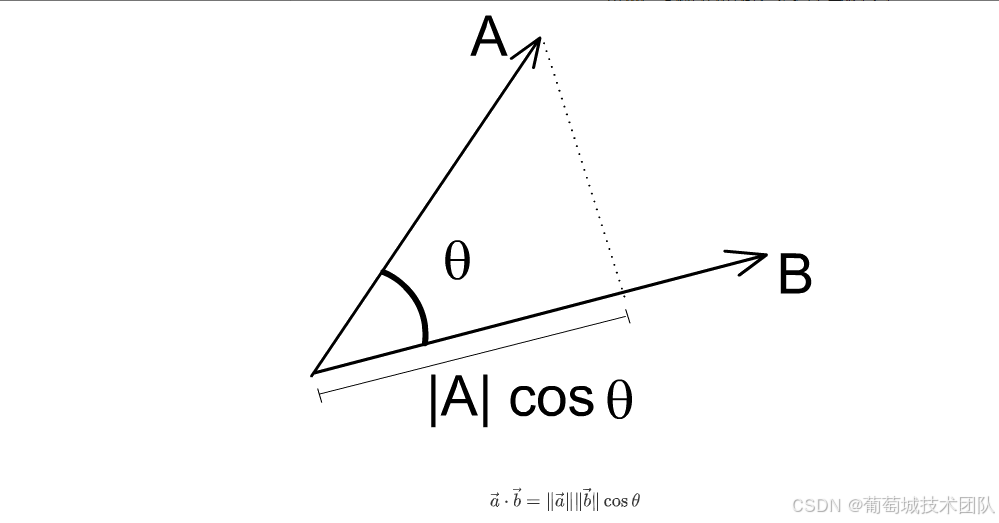
a⃗⋅b⃗=∥a⃗∥∥b⃗∥cosθ \vec{a} \cdot \vec{b} = \|\vec{a}\| \|\vec{b}\| \cos\theta a⋅b=∥a∥∥b∥cosθ
llm 正是通过通过投影来使得不同词对预测token的影响不同 , 这就和我们在听别人说话时,会通过注意力放在重点词上一样,这种机制称之为注意力。
总结
这里我们大概了解了 Transformer 的结构, 这东西对能不能写好文章有啥影响呢?
- 初始概率分布实际上来自训练语料,大部分人并不是文学造诣深厚的人,只要语料的专业性和准确性没问题,都会被训练。这意味着,初始概率分布中,文学性描述匮乏、缺少诗意、大部分都在平铺直叙,而文学缺需要一些创意。
- 如果要给 llm 更多的可能,直观的可以将温度调高(如果你是用 API 调用,一般默认为1),实际上效果并不好,因为更多的还是受初始概率分布影响,温度调节带来的效果比较有限。
- 剩下的就是这个注意力机制了,不同的输入对输出的影响很大,这意味着明确的要求、细致的工作标准会让 AI 的表现变好。回顾一下这个例子,回答比第一个的心如刀绞好多了。

但是注意力机制的影响在文章变长后表现并不好,就像我希望同时听 10 个人说话,谁也听不清,而好的文章是需要宏观的全文脉络把控的。
最后总结一下:
英国艺术理论家克莱夫·贝尔 在《艺术》中提出"艺术是有意味的形式",而不可名状的情感,不同寻常的刻意偏离是 AI 跨不过去的门槛。靠着模仿名家写作风格获得的粗略仿品,无法承载我们独一无二的生命体验。 AI 或许有爆款文章,但却永远写不出好文章。
更多推荐
 已为社区贡献268条内容
已为社区贡献268条内容








所有评论(0)